Trigonometry for Game Programming – SpriteKit and Swift Tutorial: Part 1/2
Learn trigonometry for game programming using SpriteKit and Swift. You will learn the theory and then practice using trigonometry by making a space shooter game! By Bill Morefield.
Sign up/Sign in
With a free Kodeco account you can download source code, track your progress, bookmark, personalise your learner profile and more!
Create accountAlready a member of Kodeco? Sign in
Sign up/Sign in
With a free Kodeco account you can download source code, track your progress, bookmark, personalise your learner profile and more!
Create accountAlready a member of Kodeco? Sign in
Sign up/Sign in
With a free Kodeco account you can download source code, track your progress, bookmark, personalise your learner profile and more!
Create accountAlready a member of Kodeco? Sign in
Contents
Trigonometry for Game Programming – SpriteKit and Swift Tutorial: Part 1/2
40 mins
Getting Started
Your Arsenal of Functions
Begin the Trigonometry!
Radians, Degrees and Points of Reference
Bouncing Off the Walls
Blending Angles for Smooth Rotation
Using Trig to Find Your Target
Using Trig for Collision Detection
Adding Some Spin
Where to Go from Here?
Know Angle and Length, Need Sides
Know 2 Sides, Need Angle
Know 2 Sides, Need Remaining Side
Have Angle, Need Other Angle
A common misconception is that game programmers need to know a lot about math. Although calculating distances and angles does require math, it’s actually quite easy after understanding a few fundamental concepts.
In this tutorial, you’ll learn about some important trigonometric functions and how you can use them in your games. Then you’ll get some practice applying these theories by developing a simple space shooter iOS game using the SpriteKit framework.
Don’t worry if you’ve never used SpriteKit before or you plan on using a different framework for your game — the mathematics covered in this tutorial are applicable to any game engine you might choose to use.
Trigonometry. It sounds like a mouthful, but trigonometry (or trig, for short) simply means calculations with triangles (that’s where the tri comes from).
You may not have realized this, but games are full of triangles. For example, imagine you have a spaceship game and you want to calculate the distance between these two ships:

You have the X and Y position of each ship, but how can you find the length of the diagonal white line?
Well, you can simply draw a line between each ship’s center point to form a triangle like this:
Note that one of the corners of this triangle has an angle of 90 degrees. This is known as a right triangle and the triangle type that you’ll be dealing with in this tutorial.
Any time you can express something in your game as a triangle with a 90-degree right angle — such as the spatial relationship between the two sprites in the picture — you can use trigonometric functions to do calculations on them.
For example, in this spaceship game, you might want to:
All of this, and more, you can do with the trigonometry power!
First, let’s get the theory out of the way. Don’t worry, I’ll keep it short so you can get to the fun coding bits as quickly as possible.
These are the parts that make up a right triangle:

In the picture above, the diagonal side is called the hypotenuse. It always sits across the right angle and is the longest of the three sides.
The two remaining sides are called the adjacent and the opposite when seen from the triangle’s bottom-left corner.
If you look at the triangle from the top-right corner, then the adjacent and opposite sides switch places:
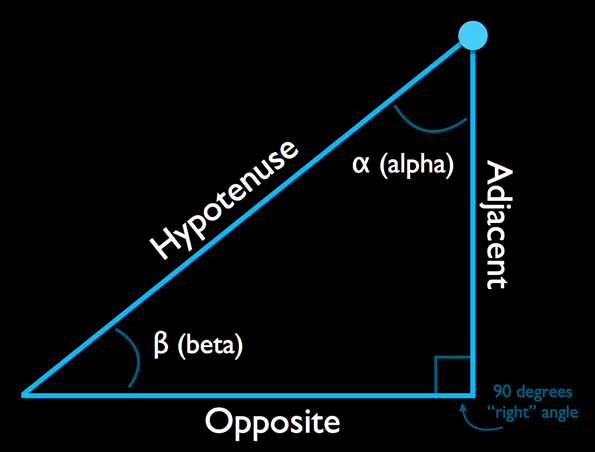
Alpha (α) and beta (β) are the names of the two other angles. You can call these angles anything you want (as long as it sounds Greek!), but usually alpha is the angle in the corner of interest and beta is the angle in the opposing corner. In other words, you label your opposite and adjacent sides with respect to alpha.
The cool thing is that if you only know a total of two elements (combination of sides and non-right angles), trigonometry allows you to find out all the remaining sides and angles using the trigonometric functions sine, cosine and tangent. For example, if you know any angle and the length of one of the sides, then you can easily derive the lengths and angles of the other sides and corners:

You can see the sine, cosine, and tangent functions (often shortened to sin, cos and tan) are just ratios. Again, if you know the alpha and the length of one of the sides, then sin, cos and tan are ratios that relate two sides and the angle together.
Think of the sin, cos and tan functions as “black boxes” – you plug in numbers and get back results. They are standard library functions, available in almost every programming language including Swift.
Let’s consider an example. Suppose the alpha angle between the ships is 45 degrees and the hypotenuse is 10 points long.

You can then plug these values into the formula:
sin(45) = opposite / 10
To solve this for the hypotenuse, you simply shift this formula around a bit:
opposite = sin(45) * 10
The sine of 45 degrees is 0.707 (rounded to three decimal places), and filling that in the forumla gives you the result:
opposite = 0.707 * 10 = 7.07
The formulas above are useful when you already know an angle, but that is not always the case – sometimes you know the length of the two side and are looking for the angle between them. To derive the angle, you can use the inverse trig functions, also known as arc functions:

If sin(a) = b, then it is also true that arcsin(b) = a. Of these inverse trig functions, you will probably use the arc tangent (arctan) the most in practice because it will help you find the hypotenuse. Sometimes these functions are written as sin-1, cos-1, and tan-1, so don’t let that confuse you.
Sometimes you may know two side lengths and you need to know third side length.
This is where geometry’s Pythagorean Theorem comes to the rescue:
a2 + b2 = c2
Or, put in terms of the triangle sides:
opposite2 + adjacent2 = hypotenuse2
If you know any two sides, calculating the third is simply a matter of filling in the formula and taking the square root. This is a very common thing to do in games and you’ll do it several times in this tutorial.
Lastly, consider the angles. If you know one of the non-right angles from the triangle, then figuring out the other one is a piece of cake. In a triangle, the sum of the three angles is always 180 degrees. Because this is a right triangle, it has a 90-degree angle. That leaves:
alpha + beta + 90 = 180
Or simply:
alpha + beta = 90
The remaining two angles must add up to 90 degrees. So if you know alpha, you can calculate beta and vice-versa.
And those are all the formulae you need to know! Which one to use in practice depends on the pieces that you already have. Usually you either have the angle and at least one side length, or you don’t have the angle but you do have two side lengths.
Enough theory. Let’s put this stuff into practice.

Use the Download Materials button at the top or bottom of this tutorial to download the starter project.
The starter project is a SpriteKit project. Build and run it on an iOS device. You’ll see there’s a spaceship that you can move around with the accelerometer along with a cannon in the center of the screen. Both sprites have a full health bar beneath them.
At the moment, the spaceship does not rotate as it moves. It would be helpful to see the where the spaceship is heading as it moves rather than having it always pointing upward. To rotate the spaceship, you need to know the angle to rotate it to. But you don’t know what that is yet; you do have the velocity vector. So how can you get an angle from a vector?
Consider what you do know. The player has the X-direction velocity length and the Y-direction velocity length:
If you rearrange these a little, you can see that they form a triangle:
Here you know the adjacent (playerVelocity.dx) and the opposite (playerVelocity.dy) side lengths.
So basically, you know the 2 sides of a right triangle, and you want to find an angle (the Know 2 Sides, Need Angle case), so you need to use one of the inverse trig functions: arcsin, arccos or arctan.
The sides you know are the opposite and adjacent sides to the angle you need. Hence, you’ll want to use the arctan function to find the ship’s rotation angle. Remember, that looks like the following:
angle = arctan(opposite / adjacent)
The Swift standard library includes an atan() function that computes the arc tangent, but it has a couple of limitations. First, the x / y yields exactly the same value as -x / -y, which means that you’ll get the same angle output for opposite velocities. Second, the angle inside the triangle isn’t exactly the one you want anyway — you want the angle relative to one particular axis, which may be 90, 180 or 270 degrees offset from the angle returned by atan().
You could write a four-way if statement to work out the correct angle by taking into account the velocity signs to determine which quadrant the angle is in, and then apply the correct offset. But, there’s a much simpler way:
For this specific problem, instead of using atan(), it’s simpler to use the function atan2(_:_:), which takes the x and y components as separate parameters, and correctly determines the overall rotation angle.
angle = atan2(opposite, adjacent)
Add the following code to the end of updatePlayer(_:) in GameScene.swift:
Notice that the Y-coordinate goes first. Remember the first parameter is the opposite side. In this case, the Y coordinate lies opposite the angle you’re trying to measure.
Build and run the app to try it out:
Hmm, this doesn’t seem to be working quite right. The spaceship certainly rotates but it’s pointing in a different direction than where it’s heading!
Here’s what’s happening: the spaceship sprite image points straight up, which corresponds to the default rotation value of 0 degrees. But by mathematical convention, an angle of 0 degrees doesn’t point upward, but to the right, along the X-axis:
To fix this, subtract 90 degrees from the rotation angle:
Try it out…
Nope! If anything, it’s even worse now! What’s missing?
Normal humans tend to think of angles as values between 0 and 360 (degrees). Mathematicians usually measure angles in radians, which are expressed in terms of π (the Greek letter Pi, which sounds like “pie” but doesn’t taste as good).
One radian is the angle you get when you travel the length of radius along the circle arc. You can do that 2π times (roughly 6.28 times) before you end up at the beginning of the circle again.
Notice the radius (straight yellow line) is the same length as the arc (red curved line). That magic angle where the two lengths are equal is one radian!
So while you may see angle values from 0 to 360, you can also see them from 0 to 2π. Most computer math functions work in radians. SpriteKit uses radians for all its angular measurements as well. The atan2(_:_:) function returns a value in radians, but you’ve tried to offset that angle by 90 degrees.
Since you will be working with both radians and degrees, it will be useful to have a way to easily convert between the two. The conversion is pretty simple. Since there are 2π radians or 360 degrees in a circle, π equates to 180 degrees. To convert radians to degrees, you divide by π and multiply by 180. To convert degrees to radians, you divide by 180 and multiply by π.
Add the following two constants above GameScene:
Finally, edit the rotation code in updatePlayer(_:) to use the degreesToRadians multiplier:
Build and run again. You’ll see that the spaceship finally rotates and faces the direction it is heading.
You have a spaceship that you can move using the accelerometers. You’re using trig to make it point in the direction it’s heading.
Having the spaceship get stuck on the edges of the screen isn’t very satisfying, and you’re going to fix that by making it bounce off the screen borders instead!
First, delete these lines from updatePlayer(_:):
And replace them with the following:
This checks whether the spaceship hit any of the screen borders, and if so, sets a Bool variable to true. But what to do after such a collision takes place? To make the spaceship bounce off the border you reverse its velocity and acceleration.
Add the following lines to updatePlayer(_:), directly below the code you just added:
If a collision is registered, you invert the acceleration and velocity values, causing the ship to bounce away again.
Build and run to try it out.
The bouncing works, but it seems a bit energetic. The problem is that you wouldn’t expect a spaceship to bounce like a rubber ball — it should lose most of its energy upon collision, and bounce off with less velocity than it had beforehand.
Add another constant right beneath let maxPlayerSpeed: CGFloat = 200:
Now, replace the code you just added to updatePlayer(_:) with the following:
You’re now mutliplying the acceleration and velocity by a damping value, bordercollisionDamping. This allows you to control how much energy is lost in the collision. In this case, you make the spaceship retain only 40% of its speed after bumping into the screen edges.
For fun, play with the value of bordercollisionDamping to see the effect of different values for this constant. If you make it larger than 1.0, the spaceship actually gains energy from the collision!
You may have noticed a slight problem: Keep the spaceship aimed at the bottom of the screen so that it continues smashing into the border over and over, and you’ll see that it starts to stutter between pointing up and pointing down.
Using the arc tangent to find the angle between a pair of X and Y components works well only if those X and Y values are fairly large. In this case, the damping factor has reduced the speed to almost zero. When you apply atan2(_:_:) to very small values, even a tiny change in these values can result in a big change in the resulting angle.
One way to fix this is to not change the angle when the speed is very slow. That sounds like an excellent reason to give a call to your old friend, Pythagoras.
Right now you don’t actually store the ship’s speed. Instead, you store the velocity, which is the vector equivalent (see here for an explanation of the difference between speed and velocity), with one component in the X-direction and one in the Y-direction. But in order to draw any conclusions about the ship’s speed (such as whether it’s too slow to be worth rotating the ship) you need to combine these X and Y speed components into a single scalar value.
Here you are in the Know 2 Sides, Need Remaining Side case, discussed earlier.
As you can see, the true speed of the spaceship — how many points it moves across the screen per second — is the hypotenuse of the triangle that is formed by the speed in the X-direction and the speed in the Y-direction.
Put in terms of the Pythagorean formula:
true speed = √(playerVelocity.dx2 + playerVelocity.dy2)
Remove this block of code from updatePlayer(_:):
And replace it with this:
Build and run. You’ll see the spaceship rotation seems a lot more stable at the edges of the screen. If you’re wondering where the value 40 came from, the answer is: experimentation. Putting print() statements into the code to look at the speeds at which the craft typically hit the borders has helped tweak this value until it felt right :]
Of course, fixing one thing breaks something else. Try slowing down the spaceship until it has stopped, then flip the device so the spaceship has to turn around and fly the other way.
Previously, that would happen with a nice animation where you actually saw the ship turning. But because you just added some code that prevents the ship from changing its angle at low speeds, the turn is now very abrupt. It’s a small detail, but it’s these details that make great apps and games.
The fix is to not switch to the new angle immediately, but to gradually blend it with the previous angle over a series of successive frames. This re-introduces the turning animation while preventing the ship from rotating when it is not moving fast enough.
This “blending” sounds fancy, but it’s actually quite easy to implement. It will require you to keep track of the spaceship’s angle between updates. Add the following property in the GameScene class:
Replace the lines of code starting from rotationThreshold declaration to the end of the last if statement in updatePlayer(_:) to the following:
The playerAngle combines the new angle and its previous angle by multiplying them with a blend factor. In other words, the new angle only contributes 20% towards the actual rotation that you set on the spaceship. Over time, more new angles get added and the spaceship eventually points in the direction it is heading.
Build and run to verify that there is no longer an abrupt change from one rotation angle to another.

Now try flying in a circle, both clockwise and counterclockwise. You’ll notice that at some point in the turn, the spaceship suddenly spins 360 degrees in the opposite direction. It always happens at the same point in the circle. What’s going on?
The atan2(_:_:) returns and angle between +π and –π (between +180 and -180 degrees). That means that if the current angle is very close +π, and then it turns a little further, it’s going to wrap around to -π (or vice-versa).
That’s actually equivalent to the same position on the circle (just like -180 and +180 degrees are the same point), but your blending algorithm isn’t smart enough to realise that – it thinks the angle has jumped a whole 360 degrees (aka 2π radians) in one step, and it needs to spin the ship 360 degrees in the opposite direction to catch back up.

To fix it, you need to recognize when the angle crosses that threshold, and adjust playerAngle accordingly. Add a new property to the GameScene class:
Once again, replace the lines of code starting from rotationThreshold declaration to the end of the last if statement in updatePlayer(_:) to the following:
Now you’re checking the difference between the current angle and the previous angle to watch for changes over the thresholds of 0 and π (180 degrees). That should fix things right up.
Build and run. You should have no more problems with turning your spacecraft!
This is a great start — you have a spaceship moving along pretty smoothly! But so far the little spaceship’s life is too easy and carefree as that big cannon isn’t doing anything. Let’s change that.
The cannon consists of two sprites: the fixed base, and the turret that can rotate to take aim at the player. You want the cannon’s turret to point at the player at all times. To get this to work, you’ll need to figure out the angle between the turret and the player.
To figure this out, it will be very similar to the spaceship rotation calculation to face its heading direction. This time, the triangle is derived from centers of the two sprites:

Again, you can use atan2(_:_:) to calculate this angle. Add the following method inside of GameScene:
The deltaX and deltaY help measure the distance between the player sprite and the turret sprite. You plug these values into atan2(_:_:) to get the relative angle between them.
As before, you need to convert this angle to include the offset from the X-axis (90 degrees) so the sprite is oriented correctly. Remember that atan2(_:_:) always gives you the angle between the hypotenuse and the 0-degree line; it’s not the angle inside the triangle.
Add the following code to the end of update(_:):
Build and run. The turret will now always point toward the spaceship.
You can accomplish this by “blending” the old angle with the new one, just like you did with the spaceship’s rotation angle. The smaller the blend factor, the more time the turret needs to catch up with the spaceship. See if you can implement this on your own.
The spaceship can fly directly through the cannon without consequence. It would be more challenging (and realistic) if it loses health when colliding with the cannon. This is where you enter the sphere of collision detection (sorry about the pun! :]).
You could use SpriteKit’s physics engine for this, but it’s not that hard to do collision detection yourself, especially if you model the sprites using simple circles. Detecting whether two circles intersect is a piece of cake. All you have to do is calculate the distance between them (*cough* Pythagoras) and see if it is smaller than the sum of the radii of both circles.

Add two new constants right above GameScene:
These are the sizes of the collision circles around the cannon and the player. Looking at the sprite, you’ll see that the actual radius of the cannon image in pixels is slightly larger than the constant you’ve specified (around 25 points), but it’s nice to have a bit of wiggle room. You don’t want your games to be too unforgiving, or players may not find it as fun.
The fact that the spaceship isn’t circular shouldn’t deter you. A circle is often a good enough approximation for the shape of an arbitrary sprite. Due to its shape, it has the big advantage of a much simpler trig calculations. In this case, the body of the ship is roughly 20 points in diameter (remember, the diameter is twice the radius).
First, add this property to GameScene for the collision sound effect:
Add the following method to GameScene to detect collision:
You’ve seen how this has worked before. First, you calculate the distance between the X-positions of the two sprites. Second, you calculate the distance between the Y-positions of the two sprites. Treating these two values as the sides of a right triangle, you can then calculate the hypotenuse. The hypotenuse is the distance between the two sprites. If that distance is smaller than the sum of the collision radii, play the sound effect.
Add a call to this new method at the end of update(_:):
Time to build and run again. Give the collision logic a whirl by flying the spaceship into the cannon.
Notice that the sound effect plays endlessly as soon as a collision begins. That's because, while the spaceship flies over the cannon, the game registers repeated collisions, one after another. There isn’t just one collision, there are 60 per second, and it plays the sound effect for every one of them!
Collision detection is only the first half of the problem. The second half is collision response. Not only do you want audio feedback from the collision, but you also want a physical response — the spaceship should bounce off the cannon.
Add this constant to the top of GameScene.swift:
Then add these lines of code right below the guard statement in checkShipCannonCollision():
This is very similar to what you did to make the spaceship bounce off the screen borders. Build and run to see how it works.
It looks pretty good if the spaceship is going fast when it hits the cannon. But if it's moving too slowly, then even after reversing the speed, the ship sometimes stays within the collision radius and never makes its way out of it. Clearly, this solution has some problems.
Instead of just bouncing the ship off the cannon by reversing its velocity, you need to physically push the ship away from the cannon by adjusting its position so that the radii no longer overlap.
To do this, you'll need to calculate the vector between the cannon and the spaceship. Fortunately, you have calculated this earlier to measure the distance between them. So how do you use that distance vector to move the ship?
The vector formed by deltaX and deltaY is already pointing in the right direction, but it's the wrong length. The length you need it to be is the difference between the radii of the ships and its current length. This way, when you add it to the ship's current position, the ship will no longer be overlapping the cannon.
The current length of the vector is distance, but the length that you need it to be is:
cannonCollisionRadius + playerCollisionRadius - distance
So how can you change the length of a vector?
The solution is to use a technique called normalization. You normalize a vector by dividing the X and Y components by the current scalar length (calculated using Pythagoras). The resultant "normal" vector, has an overall length of one.
Then, you just multiply the X and Y by the desired length to get the offset for the spaceship. Add the following code right under the previous lines of code you added to checkShipCannonCollision():
Build and run. You'll see the spaceship now bounces properly off the cannon.
To round off the collision logic, you'll subtract some hit points from the spaceship and the cannon. Then, update the health bars. Add the following code right before run(collisionSound):
Build and run again. The ship and cannon now lose a few hit points each time they collide.
For a nice effect, you can add some spin to the spaceship after a collision. This additional rotation doesn't influence the flight direction; it just makes the effect of the collision more profound (and the pilot more dizzy). Add a new constant to the top of GameScene.swift:
This sets the amount of spin to half a circle per second, which I think looks pretty good. Now add a new property to the GameScene class:
In checkShipCannonCollision(), add the following code just before the update the health bar methods:
Finally, add the following code to updatePlayer(_:) right before playerSprite.zRotation = playerAngle - 90 * degreesToRadians:
The playerSpin has effectively override the ship's display angle for the spin duration without affecting the velocity. The amount of spin quickly decreases over time, so that the ship comes out of the spin after one second. While spinning, you update previousAngle to match the spin angle so that the ship doesn't suddenly snap to a new angle after coming out of the spin.
Build and run and set that ship spinning!
You can download the completed version of the project so far using the Download Materials button at the top or bottom of this tutorial.
You've seen how you can use triangles to breathe life into your sprites with the various trigonometric functions to handle movement, rotation and even collision detection.
But there's more to come in Part 2 of the Trigonometry for Game Programming series: You'll add missiles to the game, learn more about sine and cosine, and see some other useful ways to put the power of trig to work in your games.
If you want to learn more about SpriteKit and games programming, read 2D Apple Games by Tutorials.
Credits: The graphics for this game are based on a free sprite set by Kenney Vleugels. The sound effects are based on samples from freesound.org.
- Have one ship shoot a laser in the direction of the other ship
- Have one ship start moving in the direction of another ship to chase
- Play a warning sound effect if an enemy ship is getting too close
- angle = arcsin(opposite/hypotenuse)
- angle = arccos(adjacent/hypotenuse)
- angle = arctan(opposite/adjacent)
let angle = atan2(playerVelocity.dy, playerVelocity.dx)
playerSprite.zRotation = angle
playerSprite.zRotation = angle - 90
let degreesToRadians = CGFloat.pi / 180
let radiansToDegrees = 180 / CGFloat.pi
playerSprite.zRotation = angle - 90 * degreesToRadians
newX = min(size.width, max(0, newX))
newY = min(size.height, max(0, newY))
var collidedWithVerticalBorder = false
var collidedWithHorizontalBorder = false
if newX < 0 {
newX = 0
collidedWithVerticalBorder = true
} else if newX > size.width {
newX = size.width
collidedWithVerticalBorder = true
}
if newY < 0 {
newY = 0
collidedWithHorizontalBorder = true
} else if newY > size.height {
newY = size.height
collidedWithHorizontalBorder = true
}
if collidedWithVerticalBorder {
playerAcceleration.dx = -playerAcceleration.dx
playerVelocity.dx = -playerVelocity.dx
playerAcceleration.dy = playerAcceleration.dy
playerVelocity.dy = playerVelocity.dy
}
if collidedWithHorizontalBorder {
playerAcceleration.dx = playerAcceleration.dx
playerVelocity.dx = playerVelocity.dx
playerAcceleration.dy = -playerAcceleration.dy
playerVelocity.dy = -playerVelocity.dy
}
let bordercollisionDamping: CGFloat = 0.4
if collidedWithVerticalBorder {
playerAcceleration.dx = -playerAcceleration.dx * bordercollisionDamping
playerVelocity.dx = -playerVelocity.dx * bordercollisionDamping
playerAcceleration.dy = playerAcceleration.dy * bordercollisionDamping
playerVelocity.dy = playerVelocity.dy * bordercollisionDamping
}
if collidedWithHorizontalBorder {
playerAcceleration.dx = playerAcceleration.dx * bordercollisionDamping
playerVelocity.dx = playerVelocity.dx * bordercollisionDamping
playerAcceleration.dy = -playerAcceleration.dy * bordercollisionDamping
playerVelocity.dy = -playerVelocity.dy * bordercollisionDamping
}
let angle = atan2(playerVelocity.dy, playerVelocity.dx)
playerSprite.zRotation = angle - 90 * degreesToRadians
let rotationThreshold: CGFloat = 40
let speed = sqrt(playerVelocity.dx * playerVelocity.dx + playerVelocity.dy * playerVelocity.dy)
if speed > rotationThreshold {
let angle = atan2(playerVelocity.dy, playerVelocity.dx)
playerSprite.zRotation = angle - 90 * degreesToRadians
}
var playerAngle: CGFloat = 0
let rotationThreshold: CGFloat = 40
let rotationBlendFactor: CGFloat = 0.2
let speed = sqrt(playerVelocity.dx * playerVelocity.dx + playerVelocity.dy * playerVelocity.dy)
if speed > rotationThreshold {
let angle = atan2(playerVelocity.dy, playerVelocity.dx)
playerAngle = angle * rotationBlendFactor + playerAngle * (1 - rotationBlendFactor)
playerSprite.zRotation = playerAngle - 90 * degreesToRadians
}
var previousAngle: CGFloat = 0
let rotationThreshold: CGFloat = 40
let rotationBlendFactor: CGFloat = 0.2
let speed = sqrt(playerVelocity.dx * playerVelocity.dx + playerVelocity.dy * playerVelocity.dy)
if speed > rotationThreshold {
let angle = atan2(playerVelocity.dy, playerVelocity.dx)
// did angle flip from +π to -π, or -π to +π?
if angle - previousAngle > CGFloat.pi {
playerAngle += 2 * CGFloat.pi
} else if previousAngle - angle > CGFloat.pi {
playerAngle -= 2 * CGFloat.pi
}
previousAngle = angle
playerAngle = angle * rotationBlendFactor + playerAngle * (1 - rotationBlendFactor)
playerSprite.zRotation = playerAngle - 90 * degreesToRadians
}
func updateTurret(_ dt: CFTimeInterval) {
let deltaX = playerSprite.position.x - turretSprite.position.x
let deltaY = playerSprite.position.y - turretSprite.position.y
let angle = atan2(deltaY, deltaX)
turretSprite.zRotation = angle - 90 * degreesToRadians
}
updateTurret(deltaTime)
let cannonCollisionRadius: CGFloat = 20
let playerCollisionRadius: CGFloat = 10
let collisionSound = SKAction.playSoundFileNamed("Collision.wav", waitForCompletion: false)
func checkShipCannonCollision() {
let deltaX = playerSprite.position.x - turretSprite.position.x
let deltaY = playerSprite.position.y - turretSprite.position.y
let distance = sqrt(deltaX * deltaX + deltaY * deltaY)
guard distance <= cannonCollisionRadius + playerCollisionRadius else { return }
run(collisionSound)
}
checkShipCannonCollision()
let collisionDamping: CGFloat = 0.8
playerAcceleration.dx = -playerAcceleration.dx * collisionDamping
playerAcceleration.dy = -playerAcceleration.dy * collisionDamping
playerVelocity.dx = -playerVelocity.dx * collisionDamping
playerVelocity.dy = -playerVelocity.dy * collisionDamping
let offsetDistance = cannonCollisionRadius + playerCollisionRadius - distance
let offsetX = deltaX / distance * offsetDistance
let offsetY = deltaY / distance * offsetDistance
playerSprite.position = CGPoint(
x: playerSprite.position.x + offsetX,
y: playerSprite.position.y + offsetY
)
playerHP = max(0, playerHP - 20)
cannonHP = max(0, cannonHP - 5)
updateHealthBar(playerHealthBar, withHealthPoints: playerHP)
updateHealthBar(cannonHealthBar, withHealthPoints: cannonHP)
let playerCollisionSpin: CGFloat = 180
var playerSpin: CGFloat = 0
playerSpin = playerCollisionSpin
if playerSpin > 0 {
playerAngle += playerSpin * degreesToRadians
previousAngle = playerAngle
playerSpin -= playerCollisionSpin * CGFloat(dt)
if playerSpin < 0 {
playerSpin = 0
}
}










